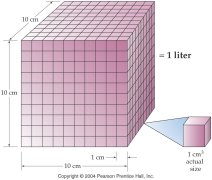
Unit Analysis Problem Solving:
Chemistry word problems sometimes may be difficult. There are several methods for solving chemical word problems. A powerful technique for solving problems is called unit analysis method, sometimes referred to as dimensional analysis method, or factor label method of problem solving. Unit analysis cannot solve every chemistry word problem, but it is very effective for the problems we encounter in beginning and college chemistry.Corwin's Text: Chapter 2 Section 2.9

How do you approach Word Problems?